| Ấn tượng bài giảng Toán từ các giáo sư Mỹ |
 |
 |
 |
| Sunday, 16 November 2025 11:06 |
|
Thứ 6 ngày 14/11 vừa qua, học sinh trường THPT chuyên Khoa học Tự nhiên rất hân hạnh được gặp mặt 2 giáo sư từ Mỹ với bài giảng về Toán do Viện Nghiên cứu cao cấp về Toán (VIASM) phối hợp với Trường tổ chức. Giáo sư Franklin Kenter và giáo sư Vân.C Nguyễn từ Khoa Toán, United States Naval Academy. Cả hai GS đều mang đến không khí cởi mở, thân thiện, giúp học sinh cảm thấy thoải mái và hứng thú trong quá trình học tập. Buổi học dự kiến diễn ra từ 13:30 - 15:30, nhưng thực tế đã kéo dài từ 13:00 đến 16:30 trong sự hưởng ứng, phấn khích của học sinh tham dự.
Phần 1: Bài giảng của giáo sư Franklin Kenter Giáo sư Franklin Kenter hiện là giảng viên United States Naval Academy. Các lĩnh vực thầy nghiên cứu bao gồm: Lý thuyết đồ thị (graph theory), Combinatorics / toán rời rạc (discrete mathematics), Optimization, trò chơi trên mạng (games on networks). Thầy chia sẻ rằng sở thích của mình là các trò chơi, nhưng việc nhìn chúng qua lăng kính toán học đôi khi khiến mọi người cảm thấy chúng kém thú vị. Từ trải nghiệm cá nhân, thầy nhận thấy rằng nếu toán học đứng riêng lẻ, vai trò của nó có thể gây tranh cãi; tuy nhiên, khi kết hợp với các lĩnh vực khác như Kinh tế, Thể thao, Trò chơi,… toán học trở thành một công cụ vô cùng mạnh mẽ.
GS Franklin bắt đầu bài giảng bằng một trò chơi. Luật chơi như sau: Các bạn học sinh chia thành nhóm 4 người mỗi đội và được phát 3 chiếc mũ màu xanh, 3 chiếc mũ màu hồng. Sẽ có một người có vai trò đội mũ lên đầu 3 người còn lại. Tuy nhiên, 3 người còn lại chỉ thấy mũ của người bên cạnh chứ không thấy mũ của bản thân. Mỗi người sẽ phải đoán màu mũ của mình. Nhiệm vụ của đội chơi là làm sao để khi mỗi người đoán mũ của mình, có ít nhất 2 người đoán đúng. Trò chơi có hai phiên bản:
Đây là một trò chơi khá đánh đố, có những đội phải mất đến 20 phút mới đưa ra câu trả lời. Nhìn chung, có nhiều cách giải được đưa ra và cách giải của các đội đều khá thông minh. Các bạn độc giả có thể thử suy nghĩ về trò chơi này nhé. Phương pháp dạy học và minh họa bằng trò chơi kể trên giúp tất cả học sinh đều tham gia vào bài giảng, khác xa cách giảng dạy thuần túy. Thầy tạo cơ hội để học sinh có thể chủ động giải quyết vấn đề, và chỉ đưa ra gợi ý khi cần. Cách tiếp cận này khuyến khích học sinh trải qua quá trình sai – sửa, từ đó ghi nhớ bài học sâu hơn và hạn chế lặp lại những sai lầm trước. Để tổng kết, giáo sư đưa ra và chứng minh 2 mệnh đề, với trò chơi kể trên, khi có N người chơi, K màu mũ, nếu mỗi người nói lần lượt, ta sẽ cứu được N - 1 người. Với bài toán khó hơn, khi tất cả mọi người nói cùng lúc, ta sẽ cứu được ⌊N/k⌋ người. Cách thầy chứng minh bài này cũng rất thú vị. Thầy sử dụng lý thuyết đồ thị, vẽ đồ thị các trạng thái, và chứng minh mỗi trạng thái có số người kì vọng cứu được đúng bằng ⌊N/k⌋ ở mỗi trạng thái.Từ đó, thầy tổng quát hóa cách giải của học sinh thành một mệnh đề phổ biến trong toán học: “Một hệ N phương trình với N ẩn sẽ luôn có một nghiệm duy nhất.”.
Kết thúc, thầy đặt ra một câu hỏi và chứng minh mang màu sắc Đại số trừu tượng: Nếu số người chơi tiến tới vô hạn, hãy chứng minh rằng số người “phải chết” vẫn là hữu hạn. Đây là một bài toán tổng quát hơn, nhưng cũng khó hình dung hơn với các học sinh. Tuy nhiên bài toán trên ít nhiều đã cho học sinh một cái nhìn rõ hơn về Đại số trừu tượng và toán cao cấp. Bài giảng của GS Franklin không chỉ mang tới kiến thức mới mẻ mà còn cho học sinh thấy được một cách tiếp cận vô cùng thú vị với giáo dục, cho học sinh được làm các ví dụ thực tế, từ đó tự mình trải nghiệm sai lầm và rút ra bài học cho bản thân. Tinh thần nhiệt huyết với Toán của thầy thực sự truyền cảm hứng cho tất cả học sinh lắng nghe bài giảng. Phần 2: Bài giảng của giáo sư Vân C. Nguyễn Giáo sư Vân C. Nguyễn hiện là giảng viên (Associate Professor) ở Khoa Toán, Học viện Hải quân Hoa Kỳ (United States Naval Academy) — một nền tảng học thuật và giáo dục quân sự nổi tiếng ở Annapolis. Trước khi về USNA, cô từng công tác ở một số vị trí học thuật khác và có nền tảng nghiên cứu sâu trong lý thuyết đại số và đại diện. GS. Vân C. Nguyễn bắt đầu bài giảng bằng một cách rất trực quan và gần gũi: mỗi học sinh được phát một tờ giấy và hướng dẫn tự gấp một tam giác đều. Từ mô hình tam giác giấy ấy, cô dẫn dắt cả lớp hình dung được các phép xoay và hoán vị trong mặt phẳng 2D — tức là xoay và lật tam giác để hình dung trực tiếp các hoán vị của ba đỉnh, rồi liên hệ chúng với các ký hiệu toán học như
Phương pháp giảng dạy của cô mang tính gợi mở: thay vì viết các công thức và bằng chứng hoàn chỉnh, cô đưa ra các ví dụ kích thích tư duy để học sinh tự khám phá ý nghĩa của công thức. Những ví dụ ngắn, thực hành trực tiếp giúp chúng ta có thể nắm chắc những khái niệm mới và đặt nền móng để có thể phát triển lên các ý tưởng, khái niệm nâng cao hơn. Một điểm sắc sảo trong bài giảng là liên hệ giữa hoán vị và nhân ma trận — một cây cầu hữu ích giữa tổ hợp và đại số tuyến tính, rất quen thuộc trong tin học. Cô Vân giải thích cách biểu diễn một hoán vị các đỉnh bằng ma trận, rồi từ đó mở rộng ra cách các hàm đó có thể được biểu diễn bằng cách nhân ma trận. Từ lập luận này, cô và thầy Franklin đã cùng đưa ra một bài toán nâng cao: thay vì biểu diễn hoán vị đỉnh bằng ma trận , liệu ta có thể tận dụng hình học không gian để “tối giản” biểu diễn xuống ma trận hay không. Bài toán này khuyến khích học sinh suy nghĩ về những mối liên hệ giữa các lĩnh vực toán khác nhau và tìm ra những cách mới để phát triển bài toán. Bên cạnh việc truyền đạt kiến thức toán học, hai giáo sư còn nhấn mạnh một thông điệp quan trọng về quá trình học: học tập không dừng lại ở việc làm đúng, mà còn nằm ở những lần vấp ngã và thất bại. Họ khuyến khích học sinh thử, sai, sửa — coi những thất bại ban đầu là nguồn học quan trọng, nơi rèn luyện trực giác và tạo ra những bài học ‘để đời’. Tinh thần này đã giúp chúng ta không ngại phát biểu ý kiến và thử nghiệm những ý tưởng mới. Qua bài giảng của GS. Vân C. Nguyễn, ta thấy một hình mẫu giảng dạy hiện đại: sử dụng những ví dụ thực tế để dẫn vào khái niệm trừu tượng, liên kết nhiều lĩnh vực toán học (tổ hợp, hình học, đại số tuyến tính), và khai thác sai sót như một phần thiết yếu của quá trình học. Bài giảng không chỉ truyền đạt kiến thức mà còn truyền cảm hứng — giúp học sinh đặt câu hỏi, tìm lời giải, và tìm hiểu về những liên hệ giữa các lĩnh vực toán khác nhau.
Cuối cùng, xin thay mặt toàn bộ học sinh đã lắng nghe bài giảng được gửi lời cảm ơn tới 2 GS vì đã dành thời gian đến đây hôm nay. Xin chúc cho công việc và cuộc sống của 2 GS sẽ suôn sẻ.
Hà Gia Minh 11A1 Toán & Trần Hữu Đức Hiếu 11A1 Tin |
| Last Updated on Sunday, 16 November 2025 22:47 |
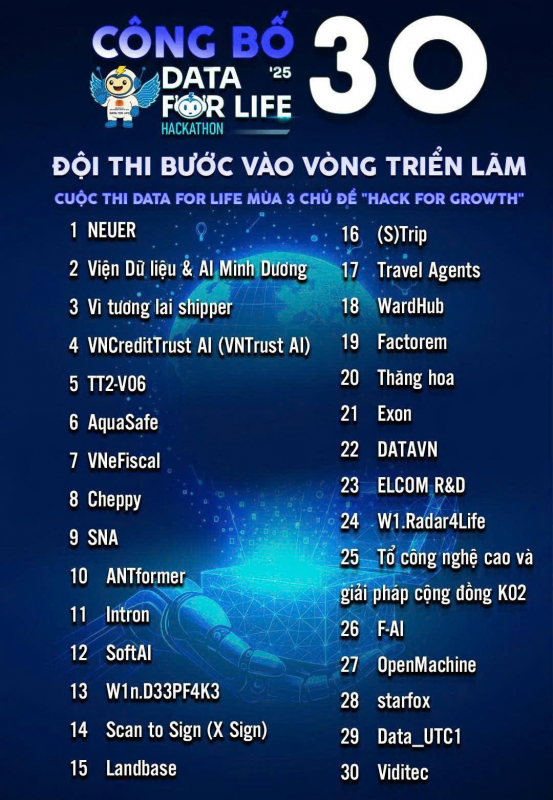
Tuyển sinh & Thi thử

Bài viết mới