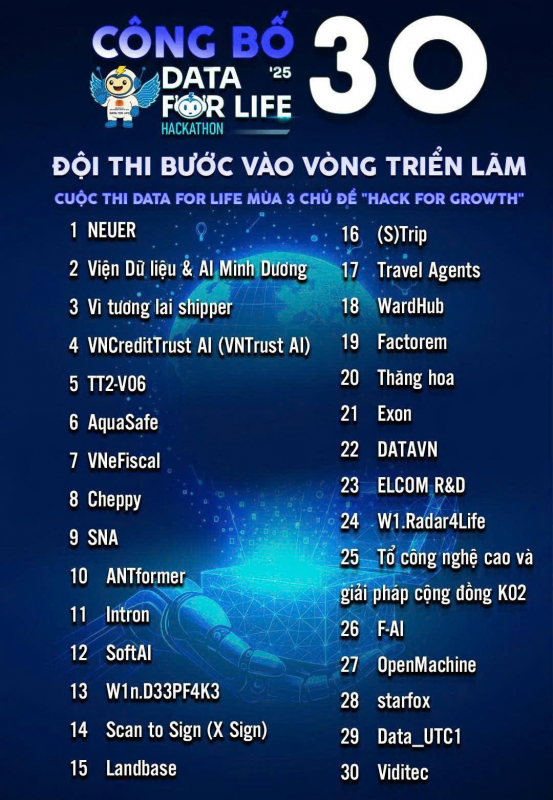
| Chuỗi bài giảng đại chúng: Toán học, Nghệ thuật và Sáng tạo |
 |
 |
 |
| Tuesday, 26 August 2025 20:39 |
|
Chiều ngày 25/8/2025, tại Trường THPT Chuyên KHTN (182 Lương Thế Vinh, Hà Nội) đã diễn ra chương trình Public Lectures Series: Mathematics, Art and Creativity, do Viện Toán Cao cấp phối hợp với Trường THPT Chuyên KHTN tổ chức.
Với những kinh nghiệm về công việc giảng dạy cũng như chuyên môn trong lĩnh vực của bản thân, hai thầy GS. Patrick Massot (Đại học Paris-Saclay, Pháp) và GS. Tadashi Tokieada (Đại học Standford, Mỹ) đã mang đến một bầu không khí học tập hấp dẫn và thú vị qua đó giúp các học sinh hiểu thêm về bản chất của toán học cùng với những ví dụ thực tiễn vô cùng gần gũi, một bài giảng với tính chuyên môn cao nhưng lại không hề nhàm chán. Không chỉ vậy những học sinh tham gia còn có cơ hội gặp mặt và nói chuyện với GS. Martin Hairer (người được trao giải thưởng Fields 2014).
Phần 1: Bài giảng của giáo sư Patrick Massot Patrick Massot là giáo sư tại Đại học Paris-Saclay (Orsay), ban đầu nghiên cứu về hình học tiếp xúc và hình học symplectic. Từ năm 2018, ông tập trung vào toán học hình thức, tức mã hóa chứng minh và định nghĩa toán học trong phần mềm proof assistant để kiểm tra tính logic và hỗ trợ giao tiếp toán học. Ông cùng đồng nghiệp đã hình thức hóa các khái niệm phức tạp như không gian perfectoid của Scholze, lý thuyết tích phân lồi của Gromov và định lý lộn cầu của Smale, một trong những kết quả nổi bật của hình học tô-pô. Hiện ông là một trong những người duy trì Mathlib (thư viện toán học của Lean) và tác giả nhiều công cụ hữu ích như LeanBlueprint. Giáo sư Patrick Massot bắt đầu bài giảng của mình bằng cách so sánh sự khác biệt giữa hình học phẳng Euclid và hình học trên các bề mặt cong. Ông chỉ ra rằng trên mặt phẳng 3 chiều, đường ngắn nhất nối hai điểm không còn là đường thẳng, ví dụ như các tuyến đường bay khi được trình chiếu trên màn hình đều có một độ “cong” nhất định. Một điều thú vị khác được giáo sư chỉ ra là một tam giác trong mặt phẳng 3 chiều có thể có tổng góc tới 270°, khác hẳn với hình học phẳng quen thuộc. Đến với phần chính của bài giảng, giáo sư giới thiệu khái niệm “độ cong”, một khái niệm mới lạ thông qua ví dụ rất trực quan: so sánh chu vi của một tờ giấy phẳng với chu vi của chính tờ giấy đó khi ép lên mặt cầu hoặc hình phao. Các bạn học sinh được mời tham gia trực tiếp vào thí nghiệm để thấy rõ hơn điều này. Theo sau đó, ông trình bày định lý Gauss–Bonnet, cho thấy tổng độ cong của một bề mặt khép kín sẽ gắn với hình dạng tôpô của bề mặt, hay số ‘lỗ’ tồn tại trên bề mặt của nó. Đây là một định lý rất quan trọng, kết nối 2 lĩnh vực tưởng chừng chẳng hề liên quan là hình học và tôpô học. Cuối cùng, bằng một thí nghiệm tưởng tượng, ông chứng minh rằng trên một hình phao luôn tồn tại ít nhất một điểm có độ cong dương, qua đó làm nổi bật mối liên hệ sâu sắc giữa trực giác hình học và các định lý toán học trừu tượng. Qua bài giảng của GS Patrick Massot, ta thấy những khái niệm toán học vốn trừu tượng như độ cong hay định lý Gauss–Bonnet được trình bày một cách gần gũi và trực quan. Những ví dụ đơn giản như tờ giấy, mặt cầu hay hình phao giúp người nghe dễ dàng hình dung và kết nối kiến thức sách vở với thực tế. Bài giảng không chỉ mở rộng hiểu biết về hình học hiện đại mà còn truyền cảm hứng trong việc tiếp cận toán học theo hướng sáng tạo và giàu hình dung trực quan. Đây thực sự là một trải nghiệm bổ ích, vừa học hỏi được kiến thức chuyên môn, vừa rèn luyện cách tư duy và cảm nhận vẻ đẹp của toán học. Phần 2: Bài giảng của giáo sư Tadashi Tokieda Giáo sư Tadashi Tokieda hiện là giáo sư Toán học tại Đại học Stanford. Ông có hành trình học thuật độc đáo: lớn lên ở Nhật Bản với tư cách một họa sĩ, sau đó trở thành nhà ngữ văn cổ điển tại Pháp, rồi lấy bằng tiến sĩ Toán học thuần túy tại Princeton và tiếp tục sự nghiệp toán học ứng dụng trên khắp thế giới. Bên cạnh nghiên cứu, ông rất tích cực phổ biến toán học ở nhiều cấp độ, đặc biệt qua Viện Toán học Châu Phi (AIMS) và kênh YouTube Numberphile. Ông cũng là diễn giả khách mời trong các bài giảng phổ biến tại ba kỳ Đại hội Toán học Quốc tế (ICM): 2018, 2022 và sắp tới 2026. GS Tadashi Tokieda đã thể hiện sự đặc biệt của mình ở ngay đầu bài giảng khi nhấn mạnh mối quan hệ hai chiều giữa Toán học và Vật lý. Đây là một đoạn dịch từ phần mở đầu của ông: “Loài người thường giỏi Vật Lý hơn Toán học. Khi một quả táo rơi xuống từ cành cây, có nhiều người có khả năng bắt lấy nó, vì họ cảm nhận trực tiếp được cách quả táo chuyển động, hơn là số người có thể tính toán quỹ đạo của nó bằng phương trình vi phân. Vì vậy, việc vận dụng các ý tưởng vật lý để khám phá và thiết lập những kết quả toán học là điều hoàn toàn tự nhiên, cho dù trong lịch sử khoa học, điều này hiếm khi được thử nghiệm.” Nếu như Toán thường được dùng để mô tả các hiện tượng vật lý thông qua phương trình, thì ngược lại, trong đời sống thực chúng ta tiếp xúc với Vật lý nhiều hơn, vì vậy việc dùng Vật lý để soi chiếu và hiểu Toán thật ra là cách tiếp cận tự nhiên hơn. Ông đưa ra nhiều ví dụ độc đáo về việc chứng minh các định lý toán học thông qua những nguyên lý vật lý quen thuộc. Chẳng hạn, định lý Pythagoras có thể được giải thích bằng momen lực qua một hình tam giác vuông được lấp đầy bằng khí; bất đẳng thức Cauchy–Schwarz được minh họa qua động lượng và ma sát; bất đẳng thức AM–GM liên hệ với định luật 2 của nhiệt động lực học. Ông cũng trình bày một cách chứng minh sự tồn tại vô hạn số nguyên tố dựa trên lập luận về “bộ nhớ hữu hạn không thể lưu vô hạn số nguyên”, và giải thích công thức Euler (V – E + F = 2) qua hiện tượng ngắn mạch một mạch điện gắn trên mặt cầu. Không chỉ có một bài giảng thú vị về toán học, GS Tokieda còn chia sẻ một số câu chuyện bên lề, gắn với trải nghiệm cá nhân và quan sát đời sống, qua đó truyền tải một bài học sâu sắc: cách nhìn nhận và tiếp cận vấn đề trong cuộc sống sẽ định nghĩa cuộc đời bạn. Ông là minh chứng sống động cho điều đó, bởi tuy đã từng trải qua nhiều lĩnh vực khác nhau, từ nghệ thuật đến ngôn ngữ học rồi đến toán học, nhưng ông cho rằng sự nghiệp của mình phát triển theo cách rất tự nhiên. Qua con mắt của xã hội, có thể việc ông làm là kì lạ nhưng ông lại thấy được sự liên kết ở các lĩnh vực tưởng chừng như khác nhau đó. Qua bài giảng của giáo sư Tadashi Tokieda, ta có thể cảm nhận được rõ sự gần gũi và sinh động trong cách ông kết nối Toán học với Vật lý. Những chứng minh vốn trừu tượng trở nên dễ hiểu và đầy thú vị nhờ các thí dụ gắn với hiện tượng tự nhiên. Bài giảng không chỉ giúp ta học thêm kiến thức mà còn truyền cảm hứng về việc nhìn toán học dưới nhiều góc độ khác nhau. Phần 3: Một số nhận định cá nhân Được tham dự chuỗi bài giảng của hai giáo sư Patrick Massot và Tadashi Tokieda là một trải nghiệm thật sự đáng nhớ. Ở bài giảng của giáo sư Patrick, tôi ấn tượng với cách ông làm sáng tỏ những khái niệm phức tạp như độ cong hay định lý Gauss–Bonnet bằng những hình ảnh rất trực quan, gần gũi. Còn giáo sư Tadashi lại khiến tôi ngạc nhiên với những chứng minh toán học dựa trên hiện tượng vật lý quen thuộc, biến những công thức khô khan thành điều sinh động và dễ hiểu. Tôi không chỉ học thêm nhiều kiến thức mới mà còn cảm nhận được sự sáng tạo và tinh tế trong cách các thầy truyền tải toán học. Đây cũng là dịp để tôi rèn luyện ngoại ngữ, mở rộng góc nhìn, và quan trọng hơn cả là nuôi dưỡng thêm tình yêu với toán học cũng như sự tò mò trước thế giới xung quanh. Ngô Mạnh Hùng (11A1 Tin), Hà Gia Minh (11A1 Toán) và Nguyễn Mai Đức Minh (11A1 Tin) |
| Last Updated on Wednesday, 27 August 2025 04:57 |
Tuyển sinh & Thi thử

Bài viết mới